剑指 Offer 36. 二叉搜索树与双向链表
题目描述
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。
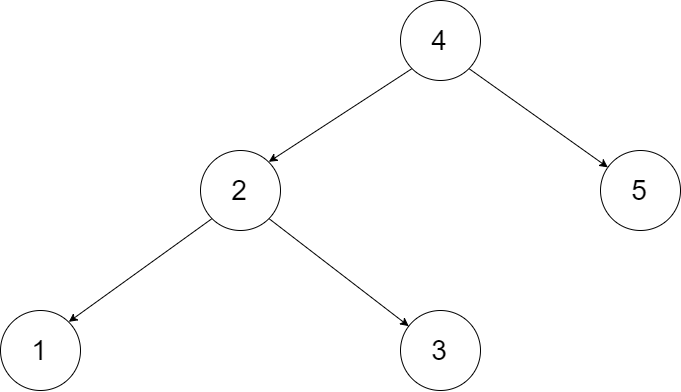
为了让您更好地理解问题,以下面的二叉搜索树为例:

我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表,第一个节点的前驱是最后一个节点,最后一个节点的后继是第一个节点。
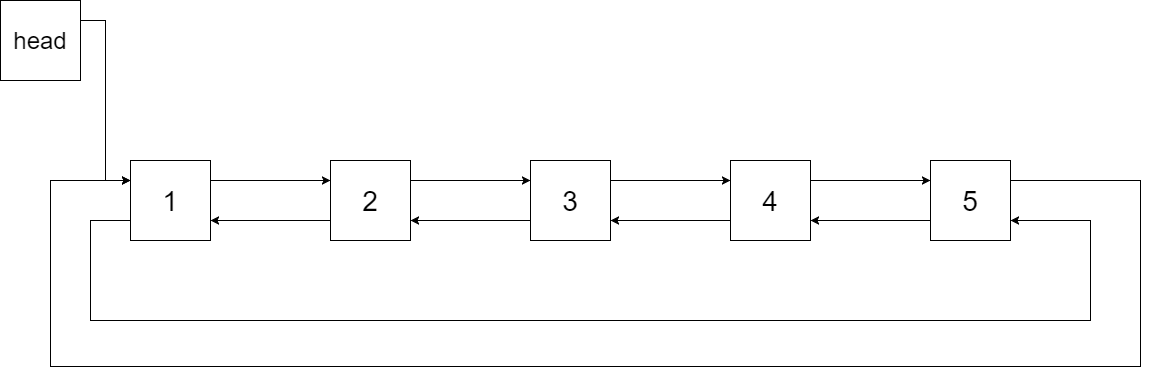
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。

特别地,我们希望可以就地完成转换操作。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。
解题思路
这道题是一道关于树和链表转换的题,直接考虑用递归来完成。
用两个指针left和right来指示根节点root的左子树和右子树转换成一个有序的循环双向链表的头结点,然后根据条件判断,将left所指示的循环双向链表、root结点、right所指示的循环双向链表连接起来。在遇到空节点的时候不做任何操作,直接返回就行。
主要分为四种情况,分述如下:
left==nullptr&&right==nullptr,也就是该节点为叶子结点。
1
2
3
4
5
6
| if(left==nullptr&&right==nullptr)
{
root->right=root;
root->left=root;
head = root;
}
|
直接将根节点转换成双向循环链表返回。
left==nullptr&&right!=nullptr,左子树为空,右子树已经转换成循环双链表。
1
2
3
4
5
6
7
8
| if(left==nullptr&&right!=nullptr)
{
root->right=right;
right->left->right=root;
root->left=right->left;
right->left=root;
head = root;
}
|
也就是将根节点和右子树转换成的循环双链表拼接起来。
left!=nullptr&&right==nullptr,右子树为空,左子树已经转换成循环双链表。
1
2
3
4
5
6
7
8
| if(left!=nullptr&&right==nullptr)
{
root->left=left->left;
left->left=root;
root->left->right=root;
root->right=left;
head = left;
}
|
也就是将根节点和左子树转换成的循环双链表拼接起来。
left!=nullptr&&right!=nullptr,左右子树都已经转换成循环双链表的情况。
1
2
3
4
5
6
7
8
9
10
| if(left!=nullptr&&right!=nullptr)
{
root->left=left->left;
root->right=right;
left->left->right=root;
left->left=right->left;
left->left->right=left;
right->left=root;
head=left;
}
|
这种情况最为麻烦,需要将根节点、左子树拼接成的双向循环链表、右子树拼接成的双向循环链表都连接起来。
最终,将各部分的代码组合起来就可。
具体细节见示例代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| Node* treeToDoublyList(Node* root)
{
if(root==nullptr) return root;
Node* left=nullptr;
Node* right=nullptr;
if(root->left) left=treeToDoublyList(root->left);
if(root->right) right=treeToDoublyList(root->right);
Node* head=nullptr;
if(left==nullptr&&right==nullptr)
{
root->right=root;
root->left=root;
head = root;
}
if(left==nullptr&&right!=nullptr)
{
root->right=right;
right->left->right=root;
root->left=right->left;
right->left=root;
head = root;
}
if(left!=nullptr&&right==nullptr)
{
root->left=left->left;
left->left=root;
root->left->right=root;
root->right=left;
head = left;
}
if(left!=nullptr&&right!=nullptr)
{
root->left=left->left;
root->right=right;
left->left->right=root;
left->left=right->left;
left->left->right=left;
right->left=root;
head=left;
}
return head;
}
|
时间复杂度为:O(n),n为二叉树的结点个数
空间复杂度为:O(logn),n为二叉树的结点个数