Leetcode958. 二叉树的完全性检验

题目描述

给定一个二叉树，确定它是否是一个完全二叉树。

百度百科中对完全二叉树的定义如下：

若设二叉树的深度为 h，除第 h 层外，其它各层 (1toh−11 \quad to \quad h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。（注：第 h 层可能包含 1to2h1 \quad to \quad 2^h 个节点。）

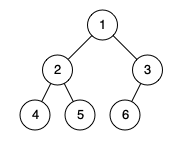
示例 1：

img

1
2
3
输入：[1,2,3,4,5,6]
输出：true
解释：最后一层前的每一层都是满的（即，结点值为 {1} 和 {2,3} 的两层），且最后一层中的所有结点（{4,5,6}）都尽可能地向左。

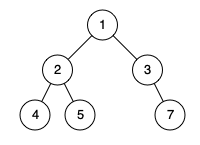
示例 2：

img

1
2
3
输入：[1,2,3,4,5,null,7]
输出：false
解释：值为 7 的结点没有尽可能靠向左侧。

提示：

  1. 树中将会有 1 到 100 个结点。

解题思路

关于完全二叉树的定义还是比较熟悉的，但是乍一看到这道题有点懵。官方题解的方法是重新同一个code变量给每一个结点标记，规则为：父节点为i的话，左孩子为2i，右孩子为2i+1。其实的根节点标记为1。最后看最右端结点的code值是不是结点的数量。这个方法当然是可行的，但是有点繁琐。

有一个更加巧妙的方法。完全二叉树如果用广度优先搜索的方法，也就是层序遍历的话，当出现一个空节点的时候，后续就不能再出现非空结点。反过来说，如果在层序遍历的过程中，在出现空节点后又出现了非空结点，那么这个二叉树一定不是完全二叉树。

据此可以写出对应的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
bool isCompleteTree(TreeNode* root)
{
    if(root==nullptr) return true;
    queue<TreeNode*>q;
    bool isNullptr=false;
    q.push(root);
    while(!q.empty())
    {
        TreeNode* cur=q.front();
        q.pop();
        if(cur==nullptr)
        {
            isNullptr=true;
            continue;
        }
        else{
            if(isNullptr)
            {
                //在空节点后又出现非空结点
                return false;
            }
            q.push(cur->left);
            q.push(cur->right);
        }
    }
    return true;
}

时间复杂度为：O(n)O(n)，nn为二叉树的结点个数

空间复杂度为：O(n)O(n)，nn为二叉树的结点个数