Leetcode221. 最大正方形
Leetcode221. 最大正方形
题目描述
在一个由 '0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积。
示例 1:
1 | 输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]] |
示例 2:
1 | 输入:matrix = [["0","1"],["1","0"]] |
示例 3:
1 | 输入:matrix = [["0"]] |
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 300matrix[i][j]为'0'或'1'
解题思路
这道题首先可以用暴力的方法来求解。比如用两层循环来扫描矩阵中的每一个元素,然后求出以[i,j]元素为左上角元素的最大正方形的面积,然后记录下这个值。当扫描完整个数组后,就可以求出最终的最大正方形面积。但是这个方法的复杂度非常高。
这道题更优的解法是运用动态规划的方法(有“最大”两个字嘛)。我们可以用 dp(i,j) 表示以 (i,j) 为右下角,且只包含 1 的正方形的边长最大值。如果我们能计算出所有 dp(i,j) 的值,那么其中的最大值即为矩阵中只包含 1 的正方形的边长最大值,其平方即为最大正方形的面积。然后需要计算dp数组 中的每个元素值:
-
如果该位置的值是
0,则,因为当前位置不可能在由1组成的正方形中; -
如果该位置的值是
1,则 的值由其上方、左方和左上方的三个相邻位置的值决定:
接下来就是最为困难的过程,如何理解上述的公式呢?
通过观察,会发现以下规律:
- 若形成正方形(非单 1),以当前元素为右下角的视角看,则需要:当前格、上、左、左上都是 1
- 可以换个角度:当前格、上、左、左上都不能受 0 的限制,才能成为正方形
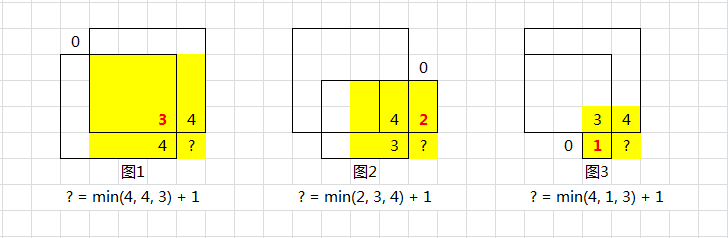
上面详解了 三者取最小 的含义:
图 1:受限于左上的 0
图 2:受限于上边的 0
图 3:受限于左边的 0
数字表示:以此为正方形右下角的最大边长
黄色表示:格子 ? 作为右下角的正方形区域
进一步的说,可以分两种情况来进行分析:
- 假设三者最小为 0 ,那么根据上图,这个位置的上方、左方和左上方的三个相邻位置的值至少有一个会为 0 ,那么当这个位置的值为 “1” ,自然以这个位置为右下角的最大正方形边长会为 1 ;
- 假设三者最小为 1 ,那么根据上图,这个位置的上方、左方和左上方的三个相邻位置的值至少有一个会为 1 ,这三个位置的
dp值都会大于等于 1 。那么当这个位置的值为 “1” ,自然以这个位置为右下角的最大正方形边长会为 2 。如果假设以这个位置为右下角的最大正方形边长大于 2 ,那么不会满足条件的,因为总会有一个方向的某个格子的值会为 ”0“(这个位置的上方、左方和左上方的三个相邻位置的值至少有一个会为 1);
上面是两种比较简单的情况,其他更大的数也是同理。
总结以下,这道题运用动态规划最大的困难是:
dp[i][j]的具体含义;- 状态转移方程的理解;
具体细节见参考代码。
参考代码
1 | int maximalSquare(vector<vector<char>>& matrix){ |
复杂度分析
时间复杂度:,其中 和 是矩阵的行数和列数
空间复杂度:,其中 和 是矩阵的行数和列数
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 二进制的叮当喵!