Leetcode470. 用 Rand7() 实现 Rand10()
Leetcode470. 用 Rand7() 实现 Rand10()
题目描述
已有方法 rand7 可生成 1 到 7 范围内的均匀随机整数,试写一个方法 rand10 生成 1 到 10 范围内的均匀随机整数。
不要使用系统的 Math.random() 方法。
示例 1:
1 | 输入: 1 |
示例 2:
1 | 输入: 2 |
示例 3:
1 | 输入: 3 |
提示:
rand7已定义。- 传入参数:
n表示rand10的调用次数。
进阶:
rand7()调用次数的 期望值 是多少 ?- 你能否尽量少调用
rand7()?
解题思路
这道题是数学题,建议想不出来直接看答案!!!
这道题相对比较复杂,我们先看一个比较简单的例子来辅助理解。
rand2()生成rand4():
假设已知rand2()可以均匀的生成[1,2]的随机数,那么如何用来均匀地生成[1,4]的随机数呢?首先,最直接的想法就是用rand2()生成两个数,将它们相加:
1 | rand2() + rand2() = ? ==>[2,4] |
这种方法有两个问题,一个是没覆盖到全部的[1,4],二是生成的数不是等概率的。所以单纯的相加是行不通的,我们需要探索新的方法。
观察上述的例子,我们尝试一些变形,比如将第一个rand2()减一后乘以2,结果如下:
1 | (rand2()-1) * 2 + rand2() = ? ==>[2,4] |
Perfect! 结果正好就是[1,4]。好像依稀看到了这个规律,但是还不真切。我们再观察一个例子:
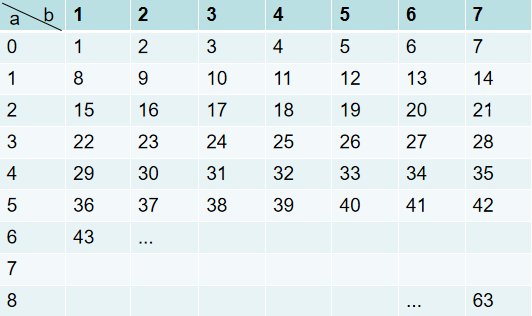
(rand9()-1) * 7 + rand7()的结果
将rand9()-1表示为a,将rand7()表示为b,结果如下表所示:
发现等概率地生成了[1,63]范围的随机数。
通过以上两个例子,我们可以尝试总结出这样一个规律:
已知 rand_N() 可以等概率的生成[1, N]范围的随机数
那么:
(rand_X() - 1) × Y + rand_Y() ==> 可以等概率的生成[1, X * Y]范围的随机数
即实现了 rand_XY()
那么,如何用上述的rand9()和rand7()来实现rand10()呢?
通过上述的例子,我们可以用rand9()和rand7()等概率地生成了[1,63]范围的随机数,但是要求等概率地生成了[1,10]范围的随机数,怎么办呢?
我们可以将61~63之间的数字舍去,然后剩下的数字就是10的倍数,然后对10取余数加1即可。这里面用到了接受-拒绝采样的思想。
然后回到这道题目上来,这时候我们就可以轻松地得出解答方法:
(rand7()-1) × 7 + rand7() ==> rand49()
这样可以等概率地生成[1,49]范围的随机数,然后舍弃41-49之间的数字,剩下的数字对10取余数加1即可。
示例代码如下:
示例代码
1 | int rand10() |
但是考虑到进阶要求,尽可能少调用 rand7() ,我们可以考虑优化一下,思路见代码注释:
1 | int rand10() { |
抄袭来源: